Penurunan Rumus tan(a + b) dan tan (a – b) - Agama tanpa ilmu pengetahuan akan buta

Written By Unknown on Monday, December 24, 2012 | Monday, December 24, 2012

sin(a + b) dan sin(a – b) dengan cos(a + b) dan cos(a – b). Tulisan kali ini yaitu tentang membuktikan sifat tan(a + b) = $\frac{tan(a)+tan(b)}{1-tan(a).tan(b)}$ dan tan(a – b) = $\frac{tan(a)-tan(b)}{1+tan(a).tan(b)}$ .

sin (a + b) = sin a cos b + cos a sin b … (i)

cos (a + b) = cos a cos b – sin a sin b … (ii)

tan (a + b) = $\frac{sin(a+b)}{cos(a+b)}$

= $\frac{sin(a).cos(b)+cos(a).sin(b)}{cos(a).cos(b)-sin(a).sin(b)}$

= $\frac{sin(a).cos(b)+cos(a).sin(b)}{cos(a).cos(b)-sin(a).sin(b)}$ x $\frac{1/[cos(a).cos(b)]}{1/[cos(a).cos(b)]}$

= $\frac{sin(a)/cos(a)+sin(b)/cos(b)}{1-sin(a).sin(b)/cos(a).cos(b)}$

= $\frac{tan(a)+tan(b)}{1-tan(a).tan(b)}$

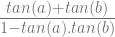
Untuk membuktikan sifat tan(a – b) dapat digunakan sifat sin (a – b) dan cos (a – b) dan jalan pembuktian serupa seperti diatas. Atau dapat juga memanfaatkan sifat tan(a + b) yang sudah dibuktikan sebelumnya yaitu dengan mengambil b = -c sehingga diperoleh