untuk membuktikan panjang garis bagi segitiga, kita akan mengkonstruksi segitiganya yaitu  ABC
dalam sebuah lingkaran, kemudian ditarik garis CD dan perpanjang
sedemikian sehingga memotong lingkaran di titik E dan membentuk
ABC
dalam sebuah lingkaran, kemudian ditarik garis CD dan perpanjang
sedemikian sehingga memotong lingkaran di titik E dan membentuk  BCE, selengkapnya perhatikan gambar dibawah ini.
BCE, selengkapnya perhatikan gambar dibawah ini.
Dari gambar diatas, diketahui AC = b, BC = a, AB = c, CD = d, AD = x, BD = y,  BAC =
BAC =  ,
,  ABC =
ABC = 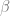 dan
dan  ACB =
ACB = 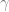 .
.
Disini kita akan membuktikan beberapa sifat untuk memperkuat pembuktian, langsung saja disimak.
a. akan dibuktikan  ACD
ACD 
 EBD
EBD
dalam pembuktian ini akan memanfaatkan sudut pusat dan sudut keliling, dimana Sudut Pusat = 2 x Sudut Keliling. Seperti yang terlihat pada gambar diatas, bahwa  AOE,
AOE,  BOE,
BOE,  BOC dan
BOC dan  AOC merupakan sudut pusat. Untuk membuktikan
AOC merupakan sudut pusat. Untuk membuktikan  ACD
ACD 
 EBD, terlebih dahulu akan ditunjukkan akan dibuktikan
EBD, terlebih dahulu akan ditunjukkan akan dibuktikan  DAC =
DAC =  DEB dan
DEB dan  DCA =
DCA =  DBE.
DBE.
Langkah Awal :
=  ACB
ACB
= 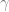
= 1/2  AOE
AOE
= 1/2  ACB
ACB
= 1/2 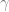
= 2 (1/2 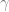 ) [karena
) [karena  BOE =
BOE =  ACB]
ACB]
= 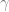
(i) akan dibuktikan  DAC =
DAC =  DEB
DEB
= 1/2  BOC
BOC
= 1/2 (2  BAC)
BAC)
= 1/2 (2  )
)
= 
Terbukti  DAC =
DAC =  DEB
DEB
(ii). akan dibuktikan  DCA =
DCA =  DBE
DBE
= 1/2  AOE
AOE
= 1/2 (2  ACE)
ACE)
= 1/2 (2  ACD)
ACD)
= 1/2 (2 . 1/2  ACB)
ACB)
= 1/2  ACB
ACB
= 1/2 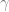
Terbukti  DCA =
DCA =  DBE
DBE
berdasarkan Teorema AAA (Angle Angle Angle), maka  ACD
ACD 
 EBD
EBD
b. akan dibuktikan  BED
BED 
 CEB (
CEB ( DEB =
DEB =  BEC dan
BEC dan  BDE =
BDE =  ADC)
ADC)
dari gambar diatas terlihat bahwa  BEC =
BEC =  DEB, dengan
DEB, dengan  DEB =
DEB =  BED
BED
= 1/2 (2  BAC)
BAC)
= 1/2 (2  )
)
= 
= 1/2  AOE
AOE
= 1/2  ACB
ACB
= 1/2 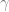
=  ACD
ACD
= 1800 – (1/2 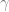 +
+  )
)
= 1800 – ( DAC +
DAC +  ACD)
ACD)
= 1800 – ( + 1/2
+ 1/2 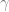 )
)
Karena  DEB =
DEB =  BEC,
BEC,  BDE =
BDE =  CBE dan
CBE dan  DBE =
DBE =  BCE. Sehingga berdasarkan Teorema AAA,
BCE. Sehingga berdasarkan Teorema AAA,  BED
BED 
 CEB.
CEB.
Karena  ACD
ACD 
 EBD, maka diperoleh
EBD, maka diperoleh
Karena  BED
BED 
 CEB, maka diperoleh
CEB, maka diperoleh
dari (1), diperoleh :
dari (2), diperoleh :
substitusi pers (3) ke pers (5), diperoleh
CE =  … (6)
… (6)
dari gambar lingkaran diatas, diketahui
DE = CE – CD
=  – d
– d
=  … (7)
… (7)
kemudian substitusi pers (4) ke pers (7), diperoleh
xy = ab – d2
Panjang Garis Bagi : d2 = ab – xy




0 comments:
Speak up your mind
Tell us what you're thinking... !