Headlines News :
Home » , » Pembuktian Integral cos x dx = sin x + C

Pembuktian Integral cos x dx = sin x + C

Written By Unknown on Monday, December 24, 2012 | Monday, December 24, 2012

membuktikan \int sin x dx = -cos x + C ? Tapi sekarang pada tulisan ini akan membuktikan \int cos x dx = sin x + C. Ide dan cara membuktikan sebenarnya sama dengan pembuktian pada tulisan sebelumnya. Tapi tidak ada salahnya saya tulis untuk menambah pengetahuan. Langsung saja perhatikan langkah-langkahnya.
\int cos x dx = sin x + C
turun-kan kedua ruas, sehingga menjadi
\frac{d}{dx} \int cos x dx = \frac{d}{dx} cos x + C
cos x = \frac{d}{dx} sin x
cos x = \frac{d}{dx} sin x
dari persamaan terakhir ini, berarti pembuktian 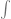\int cos x dx = -sin x ekivalen dengan membuktikan \frac{d}{dx} sin x = cos x. Disini akan dimanfaatkan Definisi Turunan.
ambil f(x) := sin x
f’(x) = lim_{h \to 0} \frac{f(x+h)-f(x)}{h}
\frac{d}{dx} cos x = lim_{h \to 0} \frac{cos(x+h)-cos(x)}{h}
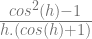= lim_{h \to 0} \frac{cos(x).cos(h)-sin(x).sin(h)-cos(x)}{h}
= lim_{h \to 0} \frac{cos(x).cos(h)-cos(x)}{h} – lim_{h \to 0} \frac{sin(x).sin(h)}{h}
= cos x lim_{h \to 0} \frac{cos(h)-1}{h} – lim_{h \to 0} \frac{sin(x).sin(h)}{h}
= cos x lim_{h \to 0} \frac{cos(h)-1}{h} \frac{cos(h)+1}{cos(h)+1} – lim_{h \to 0} \frac{sin(x).sin(h)}{h}
= cos x lim_{h \to 0} \frac{cos^2(h)-1}{h.(cos(h)+1)} – sin x lim_{h \to 0} \frac{sin(h)}{h}
= cos x lim_{h \to 0} \frac{sin^2(h)}{h.(cos(h)+1)} – sin x lim_{h \to 0} \frac{sin(h)}{h}
= cos x lim_{h \to 0} \frac{sin(h).sin(h)}{h.(cos(h)+1)} – sin x lim_{h \to 0} \frac{sin(h)}{h}
= cos x . lim_{h \to 0} sin h . lim_{h \to 0} \frac{sin(h)}{h} . lim_{h \to 0} \frac{1}{cos(h)+1} – sin x . lim_{h \to 0} \frac{sin(h)}{h}
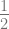= cos x . 0 . 1 . \frac{1}{2} – sin x . 1
= -sin x
Jadi terbukti \int sin u du = -cos u + C
Share this article :
Labels: ,

0 comments:

Speak up your mind

Tell us what you're thinking... !

Situs-situs Terkait

Music

 
Support : Muhammad Arwani Proudly powered by Blogger
Copyright ; 2012. Agama tanpa ilmu pengetahuan akan buta - All Rights Reserved
Copright SMK Manba'ul Huda Published by Blogger